Binary Tree Basics

LHR -> Left, Head, Right

A Simple example of a Binary Tree with LHR.

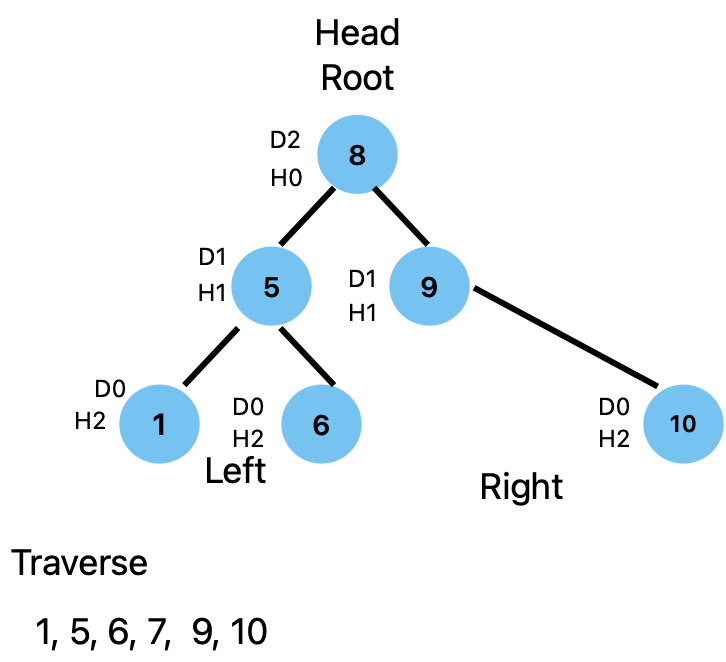
Assume that we have some values that are stored in the Binary Tree.  let's look at how we can traverse.

with LHR.

What's happening here? Dont get confused. It's simple LHR. Every node has three-pointers to it. those are LHR. you might already thought about it. yeah, it looks like a double-linked list. but it's not.

Let's go with another example.

with LHR we have two subtrees in data structure.

Left Subtree
L -> 1, 5, 6 

Root Node
H-> 7 

Right Subtree
R-> 8, 9, 10

Then the traverse will be 1, 5, 6, 7, 8, 9, 10

Depth and Height of a tree in terms of a node.

H denotes the Height of the tree

D denotes the Depth of the tree

As an example, the Root node has a Depth of 2 and a Height of 0

Successor.
with the understanding of traversing of the binary tree which is the successor of 7.
it's 8.

Predecessor.

with the understanding of traversing of the binary tree which is the predecessor of 7.
it's 6.

Every subtree ends with a right node while traversing.
in over case left subtree, it ends with 6.
and the right subtree, it starts with 8.

REMEMBER ITS NOT ARRAY.
for better understanding, we are writing down the traverse path in comma-separate.

the data is not stored sequentially, it's stored in a tree structure.

Delete a leaf node.
Simply detach the leaf node from its successor node.
for example. if we delete 1 from the structure. it will detach node from 5.

After deleting the node from the tree structure.
The traverse will be 5, 6, 7, 8, 9, 10.

Delete a Root node.
its little tricky if you delete the root node. 

In case if we have right side node.
We have to replace root node with its immediate successor. in our case 
replace 7 with 8
then delete 8;

After deleting the node from the tree structure.
Traverse will be 1, 5, 6, 7, 9, 10

else if its left sided tree.
then delete 7 there is no need of replacement.